Binary search implemented in JavaScript

Concept

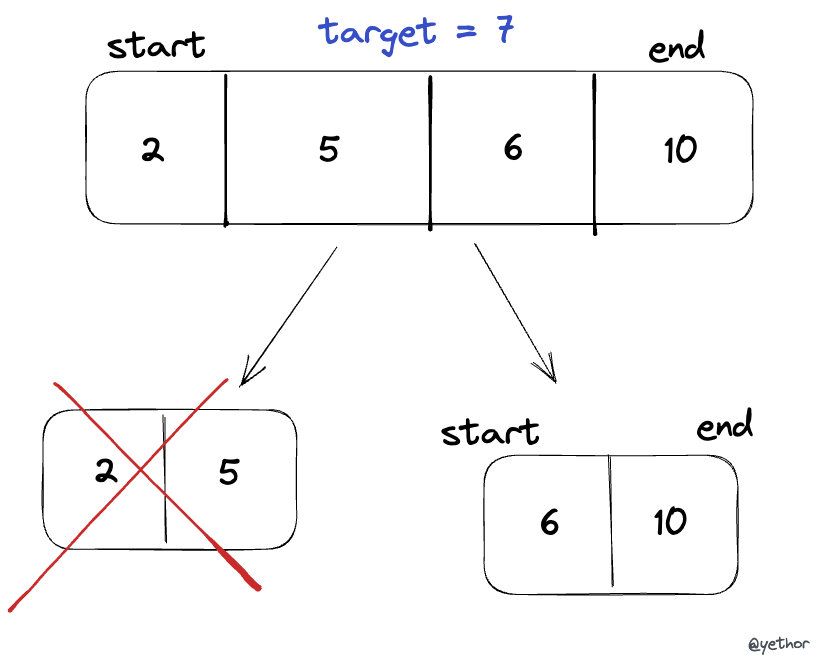
• Binary search is one of the searching algorithms that works on the Divide and Conquer Approach (divide a big problem to small sub problems)
• The main concept is to divide an array into 2 parts, take an appropriate one and keep searching
  1. If starting index is greater than ending index, return false
  2. Caculate the middle index
  3. Compare the value of middle element with target x. If they're equal, return true
  4. If middle element is greater than target x, make ending index = middle_index - 1. If it is smaller than target x, make starting index = middle_index + 1
  5. repeat step 1
• It is used to search an element in a sorted array

Implementation and Complexity

It can be implemented in two ways: recursive and iterative. Space complexity will be measured based on an auxiliary space.

Recursive Way

const recursiveFunc = (arr, x, start, end) => {
  if (end < start) return false;

  let mid = Math.floor((start + end) / 2);

  if (arr[mid] === x) return true;

  if (arr[mid] > x) {
    return recursiveFunc(arr, x, start, mid - 1);
  } else {
    return recursiveFunc(arr, x, mid + 1, end);
  }
};

Time complexity is O(log N)

• The worst case is when the searching reaches to the deepest level of the tree.
  • x is the largest number
  • x is the smallest number
  • No x is found
• In the worst case, the searching steps happens O(log N) times since it always divide the array into two parts to search the element

Space complexity is O(log N) or O(1). It depends on whether the compiler provides Tail Call Optimization

• Tail call optimization would discard the caller frame and replace the call with a jump. So if it is supported, space complexity is O(1)
• If TCO is not supported, O(log N) calls would be stacked in memory in worst case. So the space complexity is O(log N)
• Only Safari(Webkit) supports TCO using ShadowChicken, others don't

Iterative Way

const iterativeFunc = (arr, x) => {
  let start = 0;
  let end = arr.length - 1;

  while (start <= end) {
    let mid = Math.floor((start + end) / 2);

    if (arr[mid] === x) {
      return true;
    } else if (arr[mid] < x) {
      start = mid + 1;
    } else {
      end = mid - 1;
    }
  }

  return false;
};

Time complexity is O(log N) for the same reasons described in recursive way.

Space complexity is O(1)

• We only needs two space(starting index, ending index) regardless of how large the input data is